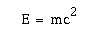Härledning av E=mc²

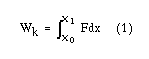
Den kanske för många mystiska formeln E=mc² är inte så svår som man kan tro. Innebörden och konsekvensen av ekvationen kan visserligen vara svår att förstå men man kan härleda den genom att utgå från den kända lagen om att Arbete (W) är Kraften (F) integrerat över sträckan ( x₀ till x₁). Vi tittar alltså på vilket arbete som utförs när en kraft (F) får verka på en kropp med massan (m) mellan det att kroppen är i vila och det att den har hastigheten (v).

Samtidigt gäller också att Arbetet (W) är skillnaden i rörelseenergi mellan x₁ och x₀. Men rörelseenergin vid x₀ är noll därför att där är kroppen i vila (vilomassan, jmf. W_k=mc²-m₀c²)
Vi kan alltså skriva följande (förväxla ej Arbetet (W) med den Kinetiska energin (W_k)):

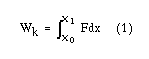
Men kraften (F) är tidsderivatan av rörelsemängden (P). Rörelsemängden är ju produkten mellan massan och hastigheten vilket innebär att om vi deriverar hastigheten så får vi accelerationen, allt enligt Newtons andra lag. Märk väl att massan (m) är den relativistiska massan och inte vilomassan (m₀).

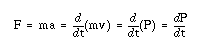
Byter vi nu kraften (F) i (1) så får vi:

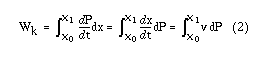
Sträckan x deriverat med avseende på tiden är ju en hastighet (v). Vad vi behöver nu är ett uttryck för dP. Vi använder oss av den relativistiska faktorn 1/sqrt(1-(v²/c²))

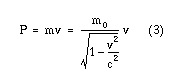
Deriverar vi nu rörelsemängden (P) m.a.p. hastigheten (v) så får vi följande:

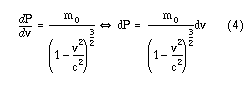
Detta sätter vi nu in i ekvation 2. Uppmärksamma att integrationsgränserna nu är hastigheterna som svarar mot sträckorna x₀ och x₁.

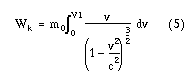
Nu löser vi integralen!

I högerledets första term ser vi uttrycket för den relativistiska massan (m) vilket medför att vi kan förenkla ekvationen avsevärt.

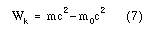
Ekvation 7 säger tydligen att den kinetiska energin för en kropp skillnaden mella mc² och m₀c². Einstein kallade uttrycket m₀c² för kroppens viloenergi, E₀=m₀c². Flyttar vi nu denna term till vänsterledet, ja då har vi samlat både rörelseenergin och viloenergin i vänster led. Vi har således ett uttryck för kroppens totala energi (E) som säger att energi och massa är ekvivalent: