En konsekvens av att ljushastigheten är konstant är att tiden måste gå olika fort för iakttagare som rör sig i förhållande till varandra.
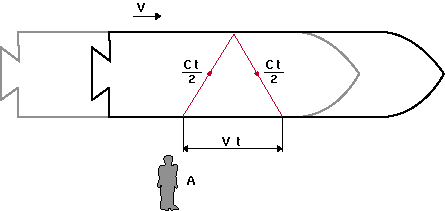
Anta att ett rymdskepp med hög fart passerar en observatör och att en ljusblixt just då sänds från rymdskeppets "golv" mot dess "tak", där en spegel reflekterar den tillbaka mot golvet (se fig 1). Ljusblixten kommer att tillryggalägga längre väg för observatören utanför skeppet än för iakttagaren inuti skeppet. Om vi tillämpar lagen om att ljushastigheten är lika stor för båda observatörerna måste observatören utanför skeppet mäta upp en längre tid för ljusblixtens färd än iakttagaren inuti skeppet*.
Man vill nu hitta ett samband mellan de olika tiderna.
Enligt observatören A utanför skeppet har ljusblixten tillryggalagt sträckan ct/2 vid sin färd tillbaka från taket till golvet (se fig 3). Här betyder c den konstanta ljushastigheten, och t är den av A uppmätta tiden för ljusets gång från golvet till taket och åter. A konstaterar vidare att skeppet under tiden t/2 har förflyttat sig sträckan vt/2, där v är skeppets hastighet relativt A. Enligt iakttagaren B inuti skeppet har ljusblixten vid återfärden från golvet till taket gått sträckan ct0/2, där t0 är den av B uppmätta tiden för ljusets tur- och returresa.

Fig 1
Vi tänker oss att ett rymdskepp med hög hastighet v passerar en observatör A på jorden. Då skeppet är mitt för A sänds en ljusblixt från skeppets golv mot en spegel i taket och åter mot golvet. För A är ljusblixtens väg den röda linjen i figuren. A registrerar tiden t för denna händelse. Ljusblixten har då tillryggalagt sträckan ct och rymdskeppet sträckan vt.
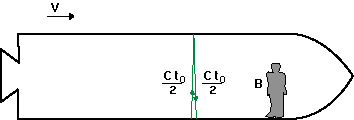
Fig 2
En iakttagare B i rymdskeppet uppmäter tiden t0 för samma skeende (ljusblixtens färd från golv till tak och åter). Enligt B har ljusblixten då tillryggalagt den med grönt markerade sträckan ct0, som är kortare än den sträcka som A observerar.
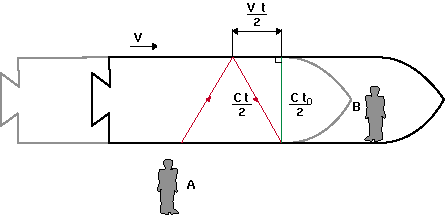
Fig 3
Ljusets återväg från taket till golvet motsvarar enligt A en förflyttning av ct/2 och enligt B förflyttningen ct0/2. Rymdskeppet har samtidigt enligt A förflyttats sträckan vt/2. Dessa tre sträckor utgör de tre sidorna i en rätvinklig triangel.
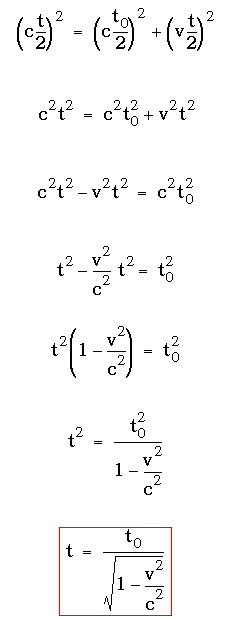 De tre sträckorna i fig.3 bildar en rätvinklig triangel. Phytagoras sats ger då den första ekvationen.
De tre sträckorna i fig.3 bildar en rätvinklig triangel. Phytagoras sats ger då den första ekvationen.
Vi tolkar innebörden av det härledda uttrycket. En iakttagare inuti rymdskeppet uppmäter tiden t0 för ljusblixtens färd från golv till tak och tillbaka igen. En observatör som ser skeppet svepa förbi med hastigheten v uppmäter en längre tid t för samma förlopp.
Sambandet gäller för alla händelseförlopp som utspelas ombord på rymdskeppet. Den tid t0 som uppmäts av besättningen på skeppet för ett sådant förlopp kallas egentiden för förloppet ifråga. Den är alltså kortare än den tid t som uppmäts för samma skeende av en observatör utanför skeppet, då skeppet rör sig i förhållande till denna observatör.
Egentiden är den kortaste tid som kan uppmätas för ett förlopp. Alla andra tider som uppmäts för samma förlopp är antingen längre eller eventuellt lika långa. Denna förlängning av tiden kallas tidsdilatation och orsakas av en relativ rörelse med hastigheten v mellan observatören och det system där förloppet utspelas.
Vid vanliga hastigheter i vårt vardagsliv är v/c ett mycket litet tal, och vi får då att t=t0.
Exprimentel prövning av tidsdilatationen.
*Istället för att observatörerna uppmäter olika gångtider för ljusblixten, skulle man kunna tänka sig att de mätte avståndet mellan golv och tak olika, så att ljusblixtens tillryggalaggda väg blev lika lång för dem båda. Följande resonemang visar dock att sträckor som är vinkelräta mot rörelseriktningen måste vara lika långa för de bägge observatörerna.
Låt oss tänka oss att rymdskeppet med mycket hög hastighet ska passera genom en tunnel med samma bredd d som skeppet har, så länge det står stilla på marken.
Antag också att en observatör på marken uppmäter ett mindre bredd än d på skeppet, när det kommer rusande mot tunneln. Enligt honom kan skeppet ta sig igenom utan att kollidera. En observatör på rymdskeppet å sin sida ser tunneln närma sig honom, och han måste då till sin fasa konstatera, att tunneln har mindre bredd än d. För honom är katastrofen oundviklig.
Lika oense om skeppets utsikter att klara passagen skulle observatörerna vara, om det rörliga föremålets bredd istället ökade.
Antingen kolliderar skeppet med tunnelmynningen eller också inte. Bara den ena av händelserna kan inträffa, och för att observatörerna ska kunna göra samma förutsägelse av vad som kommer att ske, så måste de uppmäta samma bredd bå tunneln och rymdskeppet oavsett om de befinner sig på marken eller på rymdskeppet.
Att stäckor vinkelräta mot rörelsen uppfattas olika långa är därför en orimlighet.
Tillbaka!