Several authors have studied queuing theory with a view to the analysis of the performance of computers e.g.
A key parameter, in the analysis is the probability C that an arriving customer must
wait for service, and can be calculated using "Erlang's C formula",
conveniently evaluated with a matlab program:
function C=erlang(load,m)
n=1:1:m; % number of servers
a=load*m ; % Total load: average utilization * # of servers
rho=(1./n).' * a ; % rho defined for all m
acprod=[cumprod(rho)]; % a^n/n!
C=prod(rho)./((1.-load).*(1.+sum(acprod))+load.*prod(rho)) ;
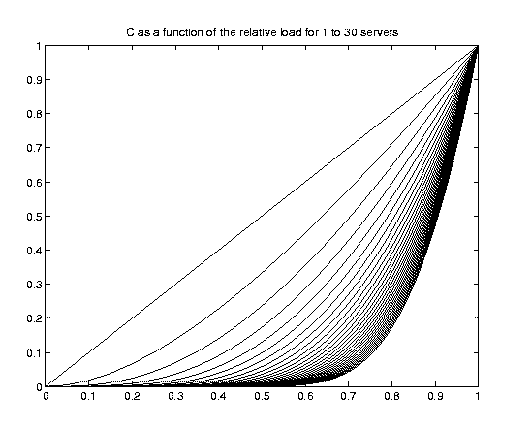
The Erlang numbers are shown, above, as a function of the relative load compares the probability to find an availabe server when the same load is distributed over server pools of various sizes.
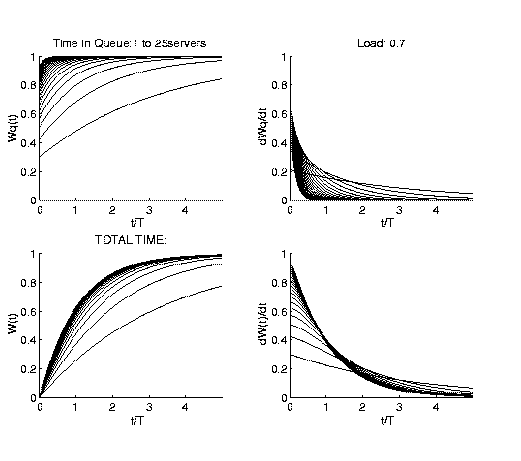
The expected waiting times (in terms of T - the average "service time") for different server pool sizes are shown (relative to the average job time) for the case of a load of 70%. Other loads and server sizes can be plotted on request.
The expectation value of the waiting time as a function of load for 1 to 10 servers is shown on a separate page.
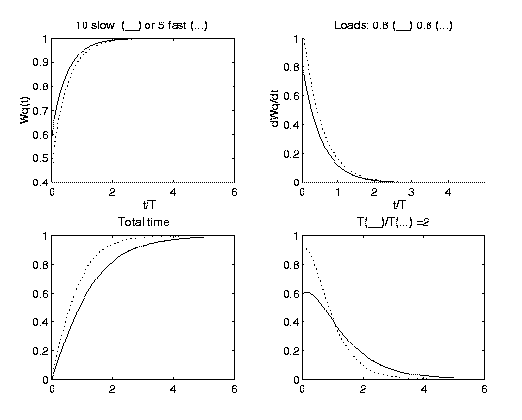
The figure above shows a comparison between
5 faster servers with 10 slower servers, with only half the speed.
The increased number of processor in itself leads to a reduction
in queueing time. However, the faster processors win when one considers
the total time in the system, including execution time.
Since faster processors lead to shorter "service times" it will
possible to sacrifice a (rather small!) part of the total capacity, without
increasing the turnaround time
if the service is provided by faster servers, as shown in the
Figure for 5 processors a factor of 1.9 faster
than the 10 slower processors.
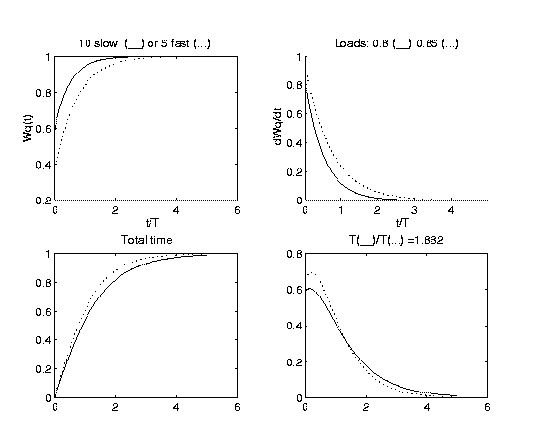
A comparison between 10 slow servers running at a load of 45% and 2 fast servers running the same jobs at a load of 90% is shown in Fig. exhibiting to some extent the advandtage of the fast servers.
These results seem to have some implications for policies on a national distribution of computing systems. The results seems to give some quantitative information about to what extent "big is beautiful". The theory, however, neglects completely psychological factors - e.g., would you like to share your computer with a bully? Many users seem to think that not-too-big is more beautiful - could this be quantified in some way?
National computing policies involve many complex issues any comments that could lead to a deeper understanding would be most welcome.
You may be interested in some of my other work and collections
related to
High-Performance Computing
<Ann-Marie.Pendrill@fy.chalmers.se>
