
Svarta hål

Radien definieras av att flykthastigheten från det avståndet är lika med ljushastigheten. Man måste alltså färdas i ljusets hastighet för att komma därifrån och eftersom man inte kan komma upp i den hastigheten kan man inte komma ut ur det svarta hålet.
Flykthastigheten beror på hur mycket rörelseenergi man måste ha för att väga upp energin hos den gravitation man utsätts för. Vi använder detta energisamband:
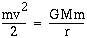
Detta ger för v = c
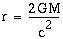
Vi ser att radien är direkt proportionell mot massan. Om man betraktar klot med samma densitet men olika vikt, t.ex. två stålkulor á ett respektive två kilo, inser man att det är volymen som är direkt proportionell mot massan - tvåkilosklotet har inte dubbelt så stor radie som enkilosklotet. Detta innebär att ett svart hål får mindre densitet om dess massa ökar.
Om vi sätter in Solens massa (Mo = 1,989×1030) får vi r = 2,953 km. Ett svart hål med Solens massa skulle alltså få en radie på ca 3 km. Därför används ofta den förenklade formeln r ~ (M/Mo)×3 km
Sätter vi in Jordens massa får vi radien 0,89 cm. Jorden skulle alltså bli mindre än två cm i diameter om den pressades samman till ett svart hål.
Densiteten är massan delat med volymen:
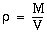
Vi har volymen (av ett klot):
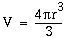
och händelsehorisontens radien (se ovan):
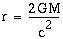
Detta ger oss densiteten:
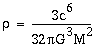
Vi ser att densiteten som krävs för att ett svart hål ska uppstå är omvänt proportionell mot kvadraten på den massa som är inblandad. Detta innebär att densiteten som behövs minskar snabbt om massan ökar.
Densiteten för ett svart hål med Solens massa är 1,85×1019 kg/m³ och för ett med Jordens 2.05×1030 kg/m³ medan den för ett hål med Vintergatans massa (ca 1011Mo) bara är ca 10-3 kg/m³ (densiteten för vatten är 10³ kg/m³). Om man har tillgång till hela Vintergatans massa behöver den alltså bara pressas samman till ett gram per kubikmeter för att ett svart hål ska uppstå!Om man inte kan trycka så hårt att ett svart hål bildas kan man kompensera det genom att skaffa mer att trycka på.
 Tillbaka
Tillbaka