Dugga, Fysiken Omkring Oss, 12 december 2006

Rita figurer. Kraftpilar skall ritas i skala. I uppgifterna nedan får g sättas till 10m/s²

1. Rita in samtliga krafter som verkar på en bil som kör med konstant hastighet uppför en backe. (1p)

2. En bil kör i 54 km/h på horisontell väg. Antag att bilen tvärbromsar och friktionskoefficienten mellan däck och väg är 1. (4p)
   1. Rita ett diagram som visar hur farten varierar med tiden under inbromsningen.
   2. Hur lång sträcka färdas bilen innan den stannar?
   3. Om bilen i stället körs in i en vägg stannar den på betydligt kortare sträcka, medan bilen deformeras. Gör ett rimligt antagande om bromssträcka. Rita in denna inbromsning i diagrammet ovan. Hur stor blir bilens acceleration under inbromsningen?
   4. Om den som åker i bilen har ett väl åtdraget säkerhetsbälte påbörjas personens inbromsningen samtidigt som bilens. Utan säkerhetsbälte påbörjas inbromsningen i stället när man träffar ratt eller instrumentpanel. Uppskatta personens bromssträcka utan bälte. Rita in även denna inbromsning i ditt diagram med rimliga antaganden.
   5. Rita ett diagram som visar samtliga krafter på passageraren under inbromsningen för någon av situationerna ovan.
   6. Hur stor blir den totala kraften från bilen på en 60 kg passagerare med och utan säkerhetsbälte, enligt dina antaganden?

3. Du sitter i en gunga och gungar så högt att repet blir horisontellt i vändlägena. Din kropp approximeras med en punktformig massa, M, repet kan betraktas som masslöst och du får bortse från luftmotstånd. Rita ut alla krafter som verkar på den som gungar: (3p)
   1. ... i vändläget
   2. ... i nedersta punkten
   3. ... när repet bildar en vinkel 30^o med horisontalplanet.

4. Du vill bestämma ett värde tyngdaccelerationen genom att bestämma svängningstiden för en pendel. Du uppskattar att osäkerheten i din längd- och tidmätning är ungefär 1%. Hur stor blir osäkerheten i ditt värde på g? Motivera ditt svar. (2p)

   

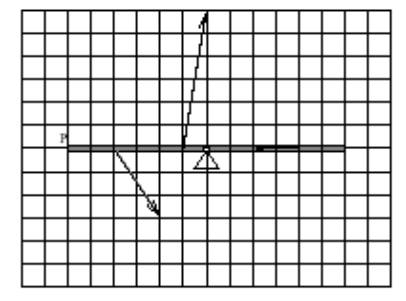
5. En stång är upphängd i sin mittpunkt, M, och påverkas, förutom av krafter i upphängningen av krafterna i figuren och en ytterligare kraft, F, i stångens ändpunkt, P. Ge villkor på F, så att stången kan hänga i jämvikt. (Låt en ruta svara mot 1N) (2p)

6. Använd dimensionsanalys för att ta fram ett samband mellan luftmotståndet på en kropp som rör sig i luft, och kroppens hastighet och yta, och luftens densitet. (2p)

7. Skriv i komponentform (låt x vara horisontellt och y vertikalt) ned de krafter som verkar på en boll när hänsyn tas till luftmotstånd. (2p)

8. En baseboll skjuts iväg. Under utskjutningen utövar basebollträt en stor kraft på bollen vilket leder till att bollen accelereras. Samtidigt utövar bollen en kraft på basebollträt. Vilken relation finns mellan dessa krafter? Under utskjutningen är den kraft basebollträt utövar på bollen (1p) ...
   1. mindre än den kraft bollen utövar på basebollträt
   2. lika stor som den kraft bollen utövar på basebollträt
   3. större än den kraft bollen utövar på basebollträt

9. Jorden befinner sig närmare solen under vinterhalvåret (på norra halvklotet). Detta kan vi t.ex. veta genom att antalet dagar under vinterhalvåret, från höstdagjämning till vårdagjämning, är färre än antalet dagar under sommarhalvåret, från vårdagjämning till höstdagjämning. Det hänger samband med bevarandet av en fysikalisk storhet. Vilken ? (1p)
   1. Energi
   2. Rörelsemängd
   3. Kraft
   4. Rörelsemängdsmoment
   5. Masscentrums läge
   6. Massa

10. Hur uppfattar du ordet "acceleration"? Gör gärna en tankekarta. Beskriv t.ex. hur ordet används i olika sammanhang, några olika typer av acceleration, vad som kan orsaka acceleration, och hur man kan mäta och uppleva den. (2p)

     

     

     

     

     

     

     

Extrauppgift om du har tid över