naturvetenskaplig Problemlösning, Feb -96
Energiförbrukning i ett hus
Uppskatta energiförbrukningen i ett
hus med längd L, bredd B, höjd S och väggtjocklek d.
Försumma värmeförluster genom golv och tak.
Välj själv väggmaterial och
lämpliga värden på L, B, S, d, inner-
och yttertemperatur.
Värmeledningen bestäms av temperaturfördelningen enligt
-
j = - k
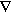 T
T
där k är värmelednings-koefficienten.
Värmeledningen kan lämligen delas upp i
x- och y- komponenter:
- jx=- k dT/dx
- jy= -k dT/dy
Exempel på värmelednings-koefficient för olika väggmaterial
finns i tabell .
Om det inte finns någon energi-tillförsel i ett
område gäller
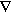 . j = 0,
vilket tillsammans med sambandet
mellan j och T
ger en ekvation för temperaturfördelningen :
. j = 0,
vilket tillsammans med sambandet
mellan j och T
ger en ekvation för temperaturfördelningen :
-
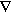 ² T = 0.
² T = 0.
Som en förövning kan man titta på en platta där
ena väggen hålls vid en högre temperatur än de övriga.
Temperaturfördelning
Bestäm först temperaturfördelningen i väggen (dvs i
x- och y-led, vi antar att fördelningen är z-oberoende)
ur ekvationen 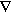 ² T = 0. Representera T(x,y) i ett
antal punkter (välj själv lämpligt antal) T(i,j),
med avstånd h mellan intill-liggande punkter.
² T = 0. Representera T(x,y) i ett
antal punkter (välj själv lämpligt antal) T(i,j),
med avstånd h mellan intill-liggande punkter.
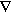 ²T kan då representeras med "finita differens"-formeln
²T kan då representeras med "finita differens"-formeln
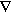 ²T(i,j) = (T(i+1,j)+T(i-1,j)
+T(i,j+1) + T(i,j-1) -4T(i,j) ) / h² +O(h²)
²T(i,j) = (T(i+1,j)+T(i-1,j)
+T(i,j+1) + T(i,j-1) -4T(i,j) ) / h² +O(h²)
Ur relationen 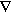 ² T = 0 följer då att
² T = 0 följer då att
- T(i,j) =(T(i+1,j) + T(i-1,j) + T(i,j+1) + T(i,j-1)) / 4
dvs. temperaturen i varje punkt kan approximeras
med medeltemperaturen hos de 4 märmsta grannarna.
Börja t.ex. med att sätta temperaturen till 0°C
för alla punkter utom på innerväggen där T sätts t.ex. till
20°C. Löp sedan över alla punkter i väggen och räkna ut
ett nytt värde på temperaturen ur
medeltemperaturen hos de 4 närmsta grannarna.
Upprepa detta tills skillnaden i temperaturfördelning
mellan två iterationer blivit tillräckligt liten! (Välj
själv lämpligt kriterium för "tillräckligt liten"!)
Åskådliggör temperaturfördelningen grafiskt!
Värmeflödet genom väggen
Värmeflödet i varje punkt bestäms av
j = - k 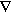 T. De olika komponenterna
av värmeflödet i en punkt (i,j) kan approximeras t.ex. med
T. De olika komponenterna
av värmeflödet i en punkt (i,j) kan approximeras t.ex. med
- jx(i,j) = -k ( T(i+1,j)-T(i,j) ) /h
- jy(i,j) = -k ( T(i,j+1)-T(i,j) ) /h
Åskådliggör gärna grafiskt värmeflödet t.ex. vid
innerväggen och/eller ytterväggen.
Värmeflödet genom ett ytelement dS
i väggen blir j·dS, dvs bara
flödet vinkelrätt mot ytan bidrar till värmeförlusterna.
Ytelementen i detta fall
väljs lämpligen med bredd = avståndet h avståndet
mellan två punkter (vi representerar då den del av väggen som ligger
på avståndet ±h/2 från en given punkt)
och höjd = takhöjden S.
Genom ett sådant ytelement på vänster vägg får vi då flödet
-jx h S, medan flödet ut genom höger vägg i stället blir
+jx h S.
Hörnen ger ett
bidrag (t.ex. med trapetsformeln).
(±jx±jy)hS /2
(där tecknen naturligtvis beror på vilket hörn som avses).
Utvidgningar
Arbeta sedan med utvidgningar av detta problem.
Frågor att undersöka kan vara
- Hur förändras temperaturfördelning och värmeflöde om
- materialet i väggarna byts
- kvoten mellan längd och bredd ändras
- väggjockleken ändras
- Hur långt ifrån hörnen märks deras påverkan på
temperaturfördelningen?
- Numerisk noggrannhet
- Vad händer om man byter steglängd, h
- Kan noggrannheten förbättras på annat sätt än att
minska steglängden?
- Hur stor steglängd behövs för att uppnå rimlig noggrannhet?
- Randvillkor: Är de antagna randvillkoren rimliga?
Skulle du kunna förbättra dem?
- Vad händer om man har en vägg bestående av två olika material
med olika värmeledningsförmåga?
Naturvetenskaplig problemlösning, Feb. 1996,
http://fy.chalmers.se/~f3aamp/matlab/hus.html
Ann-Marie.Pendrill@fy.chalmers.se
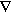 T
T
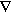 T
T
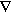 . j = 0,
vilket tillsammans med sambandet
mellan j och T
ger en ekvation för temperaturfördelningen :
. j = 0,
vilket tillsammans med sambandet
mellan j och T
ger en ekvation för temperaturfördelningen :
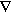 ² T = 0.
² T = 0. 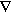 ² T = 0. Representera T(x,y) i ett
antal punkter (välj själv lämpligt antal) T(i,j),
med avstånd h mellan intill-liggande punkter.
² T = 0. Representera T(x,y) i ett
antal punkter (välj själv lämpligt antal) T(i,j),
med avstånd h mellan intill-liggande punkter.
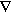 ²T kan då representeras med "finita differens"-formeln
²T kan då representeras med "finita differens"-formeln
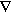 ²T(i,j) = (T(i+1,j)+T(i-1,j)
+T(i,j+1) + T(i,j-1) -4T(i,j) ) / h² +O(h²)
²T(i,j) = (T(i+1,j)+T(i-1,j)
+T(i,j+1) + T(i,j-1) -4T(i,j) ) / h² +O(h²)
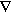 ² T = 0 följer då att
² T = 0 följer då att
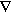 T. De olika komponenterna
av värmeflödet i en punkt (i,j) kan approximeras t.ex. med
T. De olika komponenterna
av värmeflödet i en punkt (i,j) kan approximeras t.ex. med