Naturvetenskaplig Problem-lösning

Ann-Marie Pendrill, March 1996

  1. Elektriskt fält i närheten av en atomkärna: Potentialen utanför ett sfäriskt skal med laddningen q är den samma som från en punktladdning i sfärens centrum, dvs
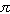
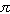
    V(r) = q/(4{pi}{eps}0) r. Inuti skalet är det elektriska fältet noll (En konsekvens av Gauss sats är att fältlinjer bara kan börja och sluta på laddningar . Innanför skalet finns inga laddnignar!) Potentialen måste då vara konstant V( r) =V ( R) =q/(4{pi}{eps}0)R om skalets radie är R.

    Denna relation kan användas tillsammans med superpositionsprincipen för att härleda ett uttryck för potentialen från en godtycklig (sfäriskt symmetrisk) laddningsfördelning: V( r) = 4 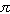{pi} * [int (p( r') r'2 /r> dr'] där r> är det stösta av avstånden r och r'. För en homogen laddningsfördelning där man har konstant laddningstäthet innanför R får man
    V( r) = q(3-(r/R)2) /2
    Utför integrationen numeriskt och jämrför resultaten. När du övertygat dig om att detta fungerar kan du prova en mera komplicerad laddningsfördelning, t.ex. Fermi-fördelningen:

    p(r) =p0 / (1 + exp((r - R)/c))

    där p0 väljs så att kärnans totala laddning blir q. Kärnans radie kan approximeras med R {=} 1.2fm A1/3 (dä:r A är masstalet) och "tjockleken" med c {=}0.55 fm.

    Beräkna på motsvarande sätt det elektriska fältet för de olika fallen. Jämför gärna den analytiska och numeriska lösningen och kontrollera att relationen E= - grad V är uppfylld.

Kommentar: Detta problem kan man komma tillbaka till i samband med kvantmekaniken och lösa vågekvationen för 1s i väte-lika system (åtminstone inne i körnan) och/eller titta på energi-skillnader pga skillnader i laddningsfördelning. Denna "isotopi-förskjutning" observeras experimentellt och kan utnyttjas för att erhålla information om skillnader i laddningsfördelning för olika isotoper.
Åskådliggör Frekvensberoendet hos i en Serie-resonanskrets. Välj sjäv lämpliga värden på R, L och C.
Fler ideer: (CSEP, ODE, tex.)