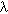 )
d
)
d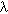 =
[ 2
=
[ 2 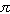 hc2 /
hc2 /
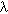 5 ]
/ (exp (hc/
5 ]
/ (exp (hc/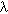 kT) -1)
d
kT) -1)
d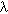
e(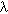 )
d
)
d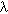 =
[ 2
=
[ 2 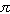 hc2 /
hc2 /
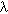 5 ]
/ (exp (hc/
5 ]
/ (exp (hc/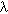 kT) -1)
d
kT) -1)
d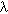
där e(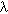 )
d
)
d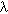 är utsträlad effekt per ytenhet inom
våglängdsområdet mellan
är utsträlad effekt per ytenhet inom
våglängdsområdet mellan
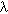 och
och 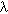 +
d
+
d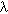 .
Värdet på de
fundementala konstanterna
c, h,
k, hämtas lämpligen
från de rekommenderade värdena, f.n.
CODATA86
.
Värdet på de
fundementala konstanterna
c, h,
k, hämtas lämpligen
från de rekommenderade värdena, f.n.
CODATA86
c=299792458; h=6.6260755E-34; k=1.380658E-23; C1=2*pi*h*c^2 lam=0.1:0.01:20; %Välj våglängdsområde! lamda=lam* 1.e-6; % i mikrometer) T=6000; %Välj temperatur es=C1./lamda.^5./(exp(h*c./(lamda*k*T) ) -1 ); plot(lamda,es)Detta skall ge en plot av strålningen från solen! Prova att byta till jordens temperatur, t.ex.
Tj=300; ej=C1./lamda.^5./(exp(h*c./(lamda*k*Tj) ) -1 ); plot(lamda,ej);För att jämföra graferna:
subplot(2,1,1) plot(lamda,es) subplot(2,1,2) plot(lamda,ej);
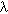 maxT=
b
=2.897 756(24) 10-3 m K
maxT=
b
=2.897 756(24) 10-3 m K
Sök maximum av e(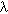 )
genom att derivera m.a.p.
)
genom att derivera m.a.p.
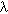 och söka nollställe.
och söka nollställe.
dedl=diff(es)./diff(lamda); subplot(1,1,1) plot(lamda(2:length(lamda)),dedl) axis([4.E-7 6.e-7 -1E20 1E20 ]) % Variera axlar för att hitta nollställe
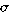 T4,
där
T4,
där 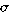 =
5.670 51(19) 10-8W m-2 K-4
=
5.670 51(19) 10-8W m-2 K-4
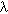 )
och jämrför
)
och jämrför
dl=lamda(2)-lamda(1); U = sum(ej) * dl % Integrera över strälningen från jorden USB=5.67051E-8 * Tj^4 %Från Stefan-Boltzmann's lag
Kanske behöver man utvidga integrationsomrädet till längre våglängder?
