Tentamen i Mekanik F del B

Tid: Tisdag 26 augusti 1997, kl. 8⁴⁵-12⁴⁵.
Lokal: MN.
Jourhavande assistent: David Gustafsson, ankn. 3173.
Hjälpmedel: TEFYMA, Standard Math Tables, Beta, Physics Handbook, valfri miniräknare samt egenhändigt skriven A4-sida.
Lösningarna anslås på institutionens anslagstavla i Fysicums trapphus samt på entrédörren till trapphuset omedelbart efter skrivningens slut. Resultatlistan anslås senast fredagen 12 september.

Förklara införda storheter och motivera ekvationer och slutsatser! Kontrollera svar m.a.p. dimension och rimlighet (krävs i förekommande fall för full poäng)! Även skisserade lösningar och fysikaliska resonemang kan poängsättas. Beskriv vad du gör! Rita!

Varje uppgift ger maximalt 15 poäng. För betyg 3,4 och 5 krävs 30, 40 resp. 50 poäng.

1. En kula glider friktionsfritt på en vertikalt ställd cirkelformad tråd, som roterar kring sin vertikala symmetriaxel med konstant rotationshastighet. Inför relevanta parametrar, och undersök huruvida det finns någon eller några dimensionslösa parametrar för systemet, något som skulle kunna indikera närvaron av olika faser, i vilka systemet beter sig kvalitativt olika. Använd Lagranges formalism för att skriva ned rörelseekvationen för kulan! Identifiera alla jämviktslägen (för godtyckliga parametervärden)! Finns någon fasövergång? Beräkna vinkelfrekvenserna för små utslag kring alla stabila jämviktslägen!

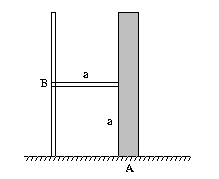2. Ett kvarnhjul är monterat enligt figuren. Hjulet kan ses som en homogen cirkelskiva, och övriga delars massor kan försummas. Det rullar utan glidning. Avgör, genom att visa på riktningar hos rörelsemängdsmoment och vridande moment, huruvida kontaktkraften i A är till beloppet större eller mindre när hjulet rullar än när det står stilla! Om den är mindre, vid vilken precessionshastighet blir den noll? Ange kraften från kulleden i B på hjulaxeln! Genomför också motsvarande resonemang/beräkningar om samma anordning rullar på ett tak istället för ett golv!

3. När man befinner sig på ett fordon som rör sig, t.ex. ett tåg eller en buss, kan man utsättas för (oönskade) tröghetskrafter (fiktiva krafter). Uppskatta, under rimliga antaganden, hur stora centrifugalkrafter och corioliskrafter man kan utsättas för, och kommentera huruvida, och i så fall vad, en konstruktör kan göra för att undvika att de blir för stora!
4. En variant av den så kallade "stavhopparparadoxen" kan formuleras sålunda: Man har byggt en "kosmisk fälla" för infångande av fientliga rymdskepp. Fällans vilolängd är densamma som rymdskeppens. P.g.a. längdkontraktionen är skeppet kortare än fällan i fällans system. När skeppet är helt och hållet inne i fällan kan dörrar i båda ändar stängas, och rymdskeppet är fångat. Från rymdskeppets synpunkt är fällan kortare, och detta är inte möjligt. Argumentera för "paradoxens" upplösning genom att visa (gärna i ett rumtidsdiagram) varför påståendet "skeppet är fångat i fällan" är subjektivt. (Tips: det kan eventuellt vara till hjälp att betrakta skeendet från ett system där de båda objekten har samma fart.)