På
svenska
På
svenskaHomepage: http://fy.chalmers.se/~f96hajo/old/home_eng.html
E-mail: f96hajo@chalmers.se Or use a formThe program shows how a list with different elements (represented by different height and color) are sorted by different sorting algorithms, i.e. demonstrate the algorithms in action. As a sorting algorithm works, the number of compares between elements and the number of swaps of elements are counted.
Adjust the pause after each swap/copying of elements. Faster to the right.
Determine the number of elements in the list. Legal values are 1 - 10 000. Press Enter/Return to execute a change.
Give the elements new values of height and color.
Give the elements new values of height and color. More elements than usual of the same color get the same height.
Reverse the order of the elements.
Save the current list. The information will be lost if the number of elements is changed.
Use the saved list a active list. This is useful when comparing different sorting algorithms, as a randomization would give different starting-conditions.
Sort the elements by value (height).
Sort the elements by color. If the elements are first sorted by value (height) and then by color, one can find out if a sorting algorithm is stable.
Used when one can't wait for an algorithm to terminate.
Start sorting by choosing a sortingmethod.
comp give the number of performed comparisions and swap give the number of elements that were exchanged.
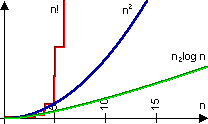The sortingmethods'
time usage is given in ordo-notation, O(n). The values cannot be used to
compare the time that different algorithms use, but can be used to determine
how intelligent or clever an algorithm is. If one knows the time-complexity
of an algorithm (e.g. that Bubblesort uses O(n2)), and the time
for the algorithm to complete for a problem of size n (e.g. the listsize
= n), one can guess what time it will use for a another problem of another
size.
Sortingalgorithms with time-complexity of O(n2) are usually called simple and the ones with time-complexity of O(n log n) are said to be advanced. For bigger problems, a more appropriate description is: O(n2) - particularly useless, O(n log n) - useful and O(n!) - simply stupid :-).
A
sortingalgorithm is said to be stable if it does not change the relative
order of elements with the same sort-key when sorting. If, for example,
the elements first are sorted by height and then by color, the elements
of the same color still are sorted by height, the sortingalgorithm is stable.
| Algorithm | Method | Time Usage | Stable |
| BubbleSort | Iterate through the list repeated times. Every step two neighbours are compared; if they are not in order, they are swapped. I've implemented the method so that for every iteration, the smallest element is bubbled down to its correct position. |
O(n2) |
Yes |
| Alternating BubbleSort | Iterate through the list repeated times. Every step two neighbours are compared, if they are not in order, they are swapped. Every other time the list is traversed forward, the other it's traversed backward. |
O(n2) |
Yes |
| InsertationSort | Iterate through the list once. The left part of the list is kept sorted and on every iteration the next element in the unsorted part of the list is put in into the sorted part, by bubbling it down the list. |
O(n2) |
Yes |
| SelectionSort | Iterate through the list once. The left part of the list contain the smallest elements of the list, in sorted order. On every iteration the smallest element in the unsorted part of the list is looked up and put right after the biggest element in the sorted list, so the sorted part grows by one element every iteration. |
O(n2) |
No |
| ShellSort | Works a lot like the notorious BubbleSort, but begin by comparing elements further apart (say half the length of the list) and decrease the comparing-distance as it runs until the distance is 0 and therefore the list is sorted. This way a rough sorting at start is accomplished. |
O(n log n) |
No |
| HeapSort | 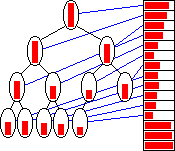 Make use of the
way complete binary trees are stored in a list. The characteristic of the
binary tree used here is that the value of every node is bigger than or
equal to the value of it's child-nodes. In every iteration we know that
the biggest element is in the first node, so it is swapped with the last
node and that way put in the correct position in the sorted part of the
list (last part). We now only have to restore the tree so it fulfills it's
characteristics (every node being bigger than it's children), and we can
go on with the next iteration. |
O(n log n) |
No |
| MergeSort |  Every pass of
the algorithm merge parts of the list together. The first pass merges parts
of length 1. The length of the parts is doubled before executing a new
pass. The list is sorted when the length of a part is bigger than the list.
The trouble with this algorithm is its need of memory during sorting, it
has to have extra memory proportional to the number of elements in the
list. |
O(n log n) |
Yes |
| QuickSort | Chooses a strategic pivot element and then place all elements smaller than the pivot to the left and all elements bigger than the pivot to the right. QuickSort is then called recursively for the left part and the right part. |
O(n log n) |
No |
| BogoSort | Bogo-sort is equivalent to repeatedly throwing a deck of cards in the air, picking them up at random, and then testing whether they are in order. It serves as a sort of canonical example of awfulness. More information can be obtained at http://www.science.uva.nl/~mes/jargon/b/bogosort.html. My implementation differs a bit from the description above, but the result is approximately the same. |
O(n!) |
No |