Home | Teaching | Publications | Research | vdWDF | Noble Surfaces | Thermodynamics | Gallery | NAISS | BNSL | MC2 | Chalmers

Computing insight on assembly at noble-metal and other surfaces

Two classes of material-surface systems stand out in terms their role of facillitating controlled experiments and thus accelerating understanding in condensed matter physics:

• All-carbon materials: graphene, graphene systems, graphitics, and their derivatives; We collective refer to these as Carbon Hill since these materials also offer exciting possibilities for development of new electronics and hence a possible alternative to silicon technology.


• Ultra-clean, well-characterized surfaces; in particular noble-metal surfaces investigated in in ultra-high vacuum and probed by, for example, scanning-tunneling microscopy (STM) or other surface-sensitive experimental techniques.

The importance of the first class systems has recently been highlighted by a Nobel Prize in physics for the discovery of graphene; the importance of the second class of system is the wealth of possibilities for STM probing and other precise characterization techniques such well-defined surface systems permits. Both classes of systems therefore defined exciting opportunities to develop science through a careful experiment-theory calibration.

First-principle calculations have long played an indispensible role in general materials physics but have had difficulties describing both the graphitics (or more generally) supramolecular problems, and most physisorption problems. This is because such systems are sparse, i.e., the materials have important regions with a sparse distribution of electrons.

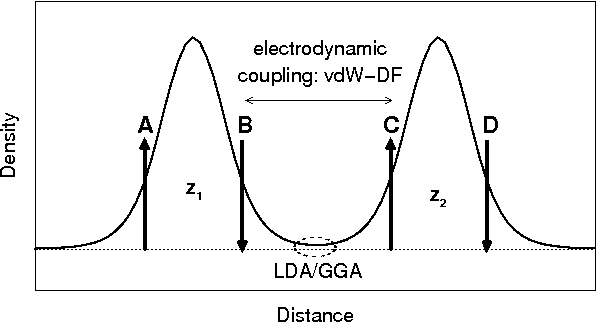
Role of van der Waals forces on the noble metal surfaces

Starting (mainly) from surface-physics theory, being electron density functional theory (DFT) developers, and recognizing the imperative need for a close experiment-theory comparison, we have at Chalmers and GU had a long-standing involvement with the both classes of systems.

A recent parameter-free and predictive theoretical account of both classes of materials-surface systems has come with our Rutgers-Chalmers development of the van der Waals Density Functional (vdW-DF) method for efficient sparse-matter DFT investigations. The vdW-DF method is a framework for consistent nonempirical evaluations of the exchange-correlation energy, going systematically beyond LDA and a GGA, reaching a true nonlocality in the description of correlations. The method is entirely based on the electron density variations and takes no other input than nuclei charges and the parameters that define constraint based LDA and GGA. The method has no need of fitting a damping function and today, the use of vdW-DF typically causes no descernable delay when compared to, for example, a standard GGA functional. The density fucntional method ahs been and is being developed in a long-standing transatlantic collaboration that began between the Rutgers research group of David C. Langreth and the Chalmers research groups of Elsebeth Schröder, of Bengt I. Lundqvist, and of Per Hyldgaard.

Sadly, David Langreth passed away in 2011. David is a dearly missed freind and a mentor to many of us. David was an outstanding condensed matter physicists who influenced our thinking in many important ways. His many-body physics formulation, with Bengt I Lundqvist and students, of the plasmon framework that underpins vdW-DF enabled the Rutgers-Chalmers collaboration to launch robust nonlocal density functionals that is meeting with broad interests. The emphasis on conservation laws and physics-based constraints suggests a high degree of transferability and the vdW-DF versions have been sucessfully tested for many different types of materials systems.

Our network of core Rutgers-Chalmers vdW-DF stakeholders also includes the research groups of Timo Thonhauser (Wake Forest), Valentino Cooper (Oak Ridge), and Kuyho Lee (Molecular Foundry, Berkeley Labs) who are also key Rutgers contributors. The group of core Rutgers-Chalmers vdW-DF stakeholders welcome questions on the method and it use. We are committed to continue to extend the method usefulness, efficientcy, and leverage, for example, by connecting vdW-DF calculations to wider materials and system modeling. The group of vdW-DF stakeholders are also continuing the method development work through many-body physics analysis and strictly within a constraint-based plasmon framework that makes the vdW-DF method a close relative of LDA and GGA.

We separately maintain an overview of Chalmers-based vdW-DF contributions since the range of vdW-DF applications is not limited to molecular adsorption (or carbon materials) but extends to the very broad class of spare matter, materials with important voids in the electron distributions.

Gallery of first-principle surface-physics results

Reflecting also on the key importance of both classes of exciting materials-surface systems, we summarize below our key First-Principle noble-metal adsorption results (while we refer to a separate presentation of our corresponding First-Principle Carbon Hill results). At these websites we collect contributions that have an address at the above-mentioned (and vdW-DF developing) Chalmers research groups.

Invited Reviews on methods, with surface-physics and growth relevance

	Density-functional bridge between surfaces and interfaces, (Lundqvist et al) Surface Science 493, 253 (2001). (preprint).
	Bridging between micro- and macroscales of materials by mesoscopic models, (Lundqvist et al) Computational Materials Science 24, 1 (2002). (preprint).
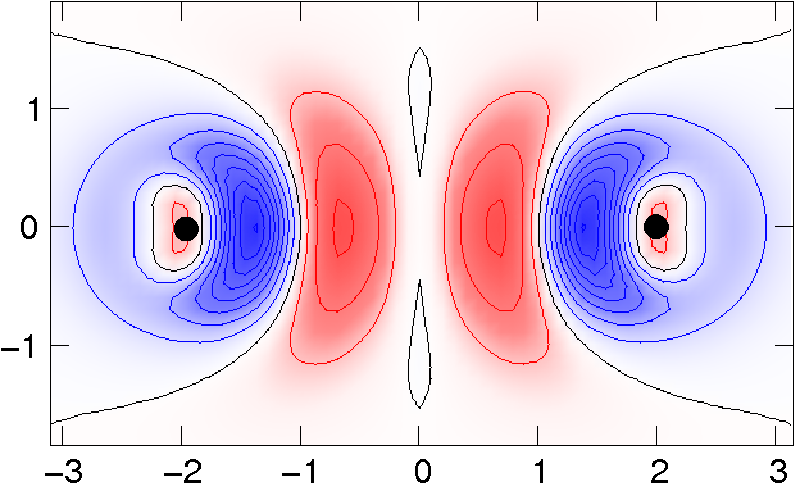
	Van der Waals Density Functional Theory with Applications (Langreth, Dion, Rydberg, Schröder, Hyldgaard, Lundqvist) International Journal of Quantum Chemistry 101, 599 (2005). preprint
	A density functional for sparse matter, (Langreth et al) Journal of Physics: Condensed Matter 21, 084203 (2009). Copyright (2009) by IoP.
	van der Waals forces in density functional theory: A review of the vdW-DF method, (Berland, Cooper, Lee, Schröder, Thonhauser, Hyldgaard, and Lundqvist) Reports of Progress in Physics 78, 066501 (2015). An invited review on the long-term research investments and progress that the van der Waals density functional (vdW-DF) method represents.

Density functional theory: Details of the vdW-DF method and more

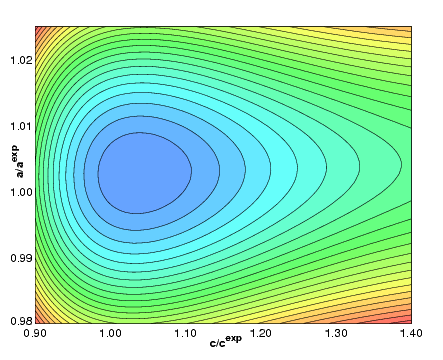	Van der Waals Density Functional for Layered Structures, (Rydberg, Dion, Jacobson, Schröder, Hyldgaard, Simak, Langreth, Lundqvist) Physical Review Letter 91, 126402 (2003). Copyright (2003) by the American Physical Society.
	Van der Waals Density Functional for General Geometries, (Dion, Rydberg, Schröder, Lundqvist, and Langreth) Physical Review Letters 92 (2004) 246401. Copyright (2004) by the American Physical Society. Erratum
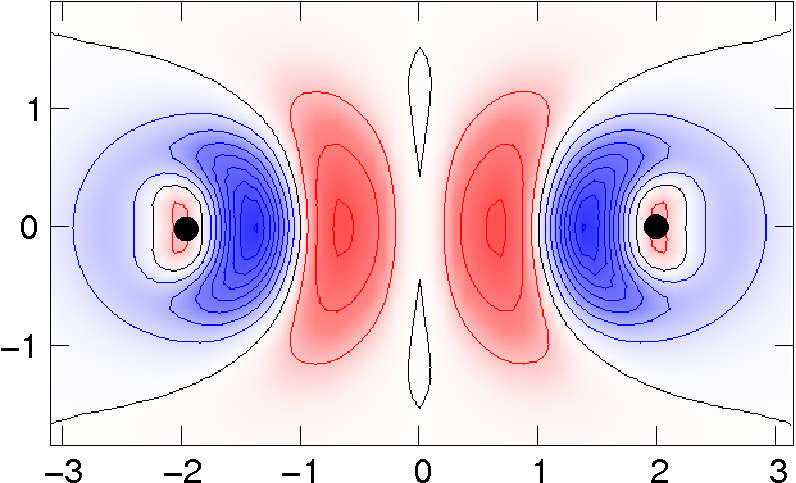	Van der Waals density functional: Self-consistent potential and the nature of the van der Waals bond, (Thonhauser, Cooper, Li, Puzder, Hyldgaard, and Langreth) Physical Review B 76, 125112 (2007). Copyright (2007) by the American Physical Society.
	Higher-accuracy van der Waals density functional, (Lee, Murray, Kong, Lundqvist, and Langreth) Physical Review B 82, 081101(R) (2010).
	Structure and binding in crystals of cage-like molecules: hexamine and platonic hydrocarbons, (Berland and Hyldgaard) Journal of Chemical Physics 132, 134705 (2010). cond-mat/1010.1487.
	Analysis of van der Waals density functional components: Binding and corrugation of benzene and C60 on boron nitride and graphene, (Berland and Hyldgaard) Physical Review B 87, 205421 (in 2013). Copyright (2013) by American Physical Society.
	Exchange functional that tests the robustness of the plasmon descripion of the van der Waals density functional, (Berland and Hyldgaard) Physical Review B 89, 035412 (2014). Copyright (2014) by the American Physical Society.
	van der Waals density functionals based on the electron-gas tradition: facing the challenge of compeeting interactions, (Berland, Arter, Cooper, Lee, Lundqvist, Schröder, Thonhauser, and Hyldgaard) Journal of Chemical Physics 140, 18A539 (2014); invited contribution to special JCP issue on ``Methods in Density Functional Theory.'' cond-mat/1403.0797.
	Interpretation of van der Waals density Functionals, (Hyldgaard, Berland and Schröder) Physical Review B 90, 075148 (2014). Copyright (2014) by the American Physical Society.
	Spin signature of nonlocal-correlation binding in metal organic frameworks, (Thonhauser, Zuluaga, Arter, Berland, Schröder, and hyldgaard) Physical Review Letters 115, 136402 (2015). Copyright (2015) by the American Physical Society.

Density functional theory: vdW-DF implementation, benchmarking, and computational strategy papers

	Potassium intercalation in graphite: A van der Waals density-functional study (Ziambaras, Kleis, Schröder, and Hyldgaard) Physical Review B 76, 155425 (2007). Copyright (2007) by the American Physical Society.
	Nature and strength of bonding in a crystal of semiconducting nanotubes: van der Waals density functional calculations and analytical results (Kleis, Hyldgaard, and Schröder) Physical Review B 77, 205422 (2008). Copyright (2008) by the American Physical Society. The article was selected to simultaneously appear in the June 2, 2008 issue of the AIP/APS Virtual Journal of Nanoscale Science & Technology.
	van der Waals density functional calculations of binding in molecular crystals, (Berland, Borck, and Hyldgaard) Computational Physics Communications 182, 1800 (2011). cond-mat/1007.3305.
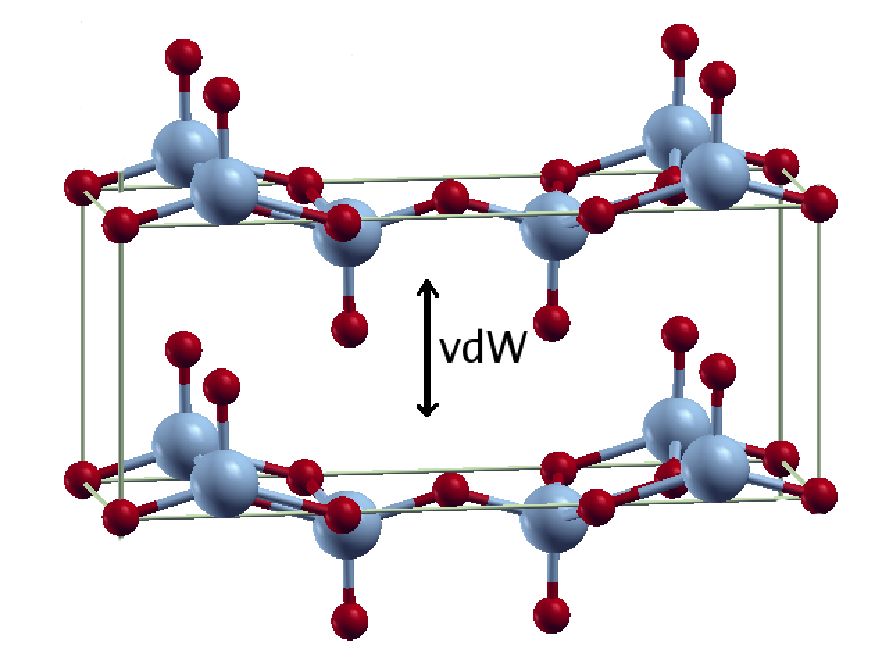	Vanadium pentoxide (V2O5): a van der Waals density functional study, (Londero and Schröder) Computer Physics Communications 182, 1805 (2011).
	Evaluation of a density functional with account of van der Waals forces using experimental data of H2 physisorption on Cu(111) (Lee, Kelkkanen, Berland, Andersson, Langreth, Schröder, Lundqvist, and Hyldgaard) Physical Review B 84, 193408 (2011). Copyright (2011) by American Physical Society.
	Benchmarking van der Waals density functionals with experimental data: potential energy curves for H2 molecules on Cu(111), (100), and (110) surfaces (Lee, Berland, Yoon, Andersson, Schröder, Hyldgaard, and Lundqvist) Journal of Physics:Condensed Matter 24, 424213 (2012). Copyright (2012) by IoP.
	Harris-type van der Waals density functional scheme, (Berland, Londero, Schröder, and Hyldgaard) Physical Review B 88, 045431 (2011). Copyright (2013) by American Physical Society.

Within and beyond canonical-ensemble ground-state density functional theory: Surface-state mediated Friedel interactions, thermodynamics and nonequilibrium tunneling

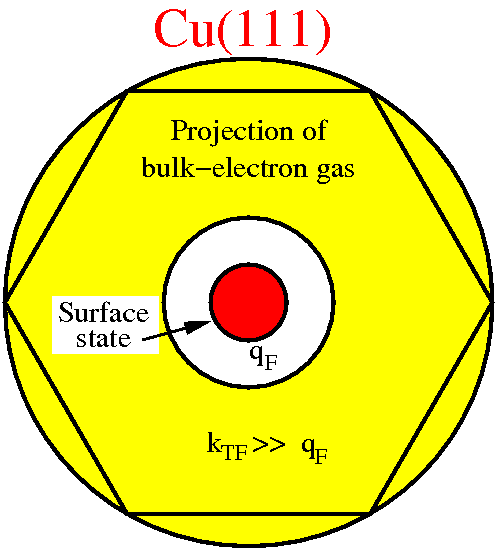	Long-ranged adsorbate-adsorbate interactions mediated by a surface-state band,, (Hyldgaard and Persson) Journal of Physics:Condensed Matter 12, L13 (2000). Copyright (2000) by IoP.
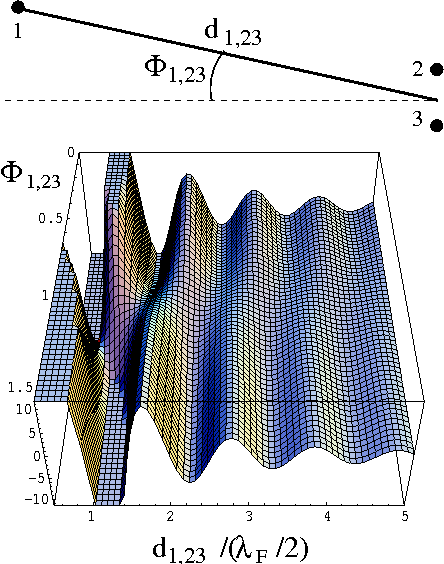	Surface-state mediated three-adsorbate interactions, (Hyldgaar and Einstein) Europhysics Letters 59, 265 (2002).
	Surface-state mediated three-adsorbate interactions: electronic nature and nanoscale consequences , (Hyldgaard and Einstein) Surface Science 532-535, 600-605 (2003). (preprint).
	Ab initio thermodynamics of deposition growth: surface terminations of CVD titanium carbide and nitride, (Rohrer and Hyldgaard) Physical Review B 82, 045415 (2010). Copyright (2010) by American Physical Society. cond-mat/1004.1929.
	Response of the Schockley surface-state to an external electrical field: A density-functional theory study of Cu(111) , (Berland, Einstein, Hyldgaard) Physical Review B 85, 035427 (2012). Copyright (2012) by the American Physical Society.
	Nonequilibrium thermodynamics of interacting tunneling transport: variational grand potential, universal density functional description, and nature of forces, (Hyldgaard) Journal of Physics:Condensed Matter 24, 424219 (2012). Copyright (2012) by IoP. cond-mat/1108.4536.

Noble-metal surface adsorptions: from adatoms to adchains

	Al Dimer Dynamics on Al(111), (Bogicevic, Hyldgaard, Wahnström and Lundqvist) Physical Review Letters 81, 172 (1998). Copyright (1998) by the American Physical Society.
	Substrate Mediated Long-Range Oscillatory Interaction between Adatoms: Cu/Cu(111), (Repp, Moresco, Meyer, Rieder, Hyldgaard, and Persson) Physical Review Letters 85, 2981 (2000). Copyright (2000) by the American Physical Society. Physical Review Focus.
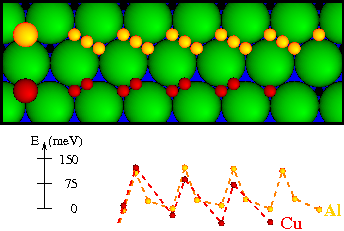	Nature, Strength, and Consquences of Indirect Adsorbate Interactions on Metals, (Bogicevic, Ovesson, Hyldgaard, Lundqvist, Brune, and Jennison) Physical Review Letters 85, 1910 (2000). Copyright (2000) by the American Physical Society.
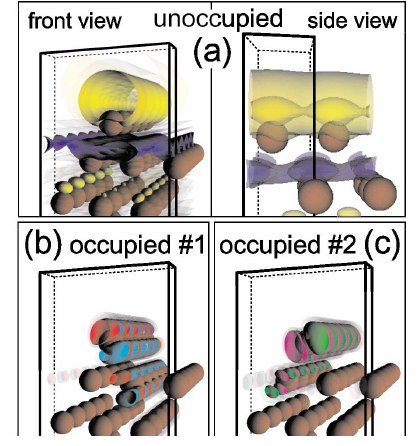	Quantum confinement in monatomic Cu chains on Cu(111) (Fölsch, Hyldgaard, Koch, and Ploog) Physical Review Letters 92, 056803 (2004). Copyright (2004) by the American Physical Society.
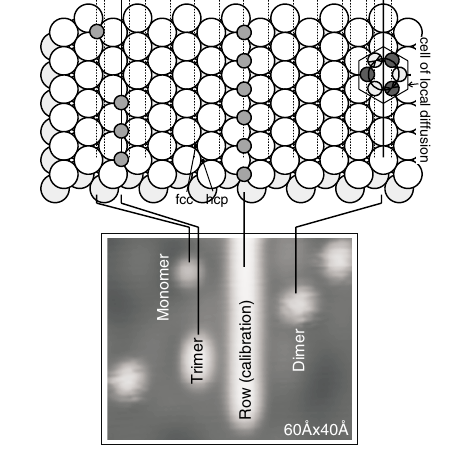	Site determination and thermally assisted tunneling in homogeneous nucleation (Repp, Meyer, Rieder, and hyldgaard) Physical Review Letters 91, 206102 (2003). Copyright (2003) by the American Physical Society.

Noble-metal surface adsorptions: molecular adsorption, interactions and assembly

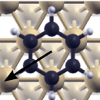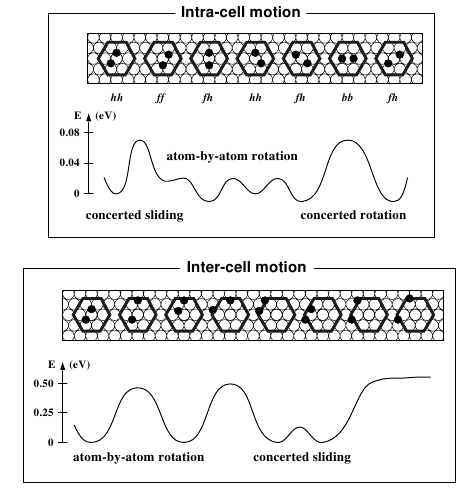
	Rings sliding on a honeycomb network: Adsorption contours, interactions, and assembly of benzene on Cu(111), (Berland, Einstein, Hyldgaard) Physical Review B 80, 155431 (2009). Copyright (2009) by the American Physical Society. The article was selected to simultaneously appear in the October 26, 2009 issue of the AIP/APS Virtual Journal of Nanoscale Science & Technology.
	Effective Elastic Properties of a Molecular Monolayer at a Metal Surface , (Sun, Kim, Le, Borck, Berland, Kim, Lu, Luo, Cheng, Einstein, Rahman, Hyldgaard, Bartels) Physical Review B 82, 201410(R) (2010). Copyright (2010) by the American Physical Society.
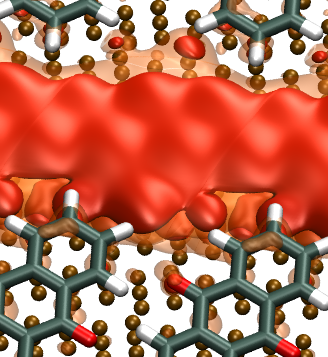	Do two-dimensional "Noble Gas Atoms" Produce Molecular Honeycombs at a Metal Surface, (Wyrick, Kim, Sun, Cheng, Lu, Zhu, Berland, Kim, Rotenberg, M. Luo, Hyldgaard, Einstein, Bartels) Nano Letters 11, 2944 (2011).

Adsorptions on other surfaces

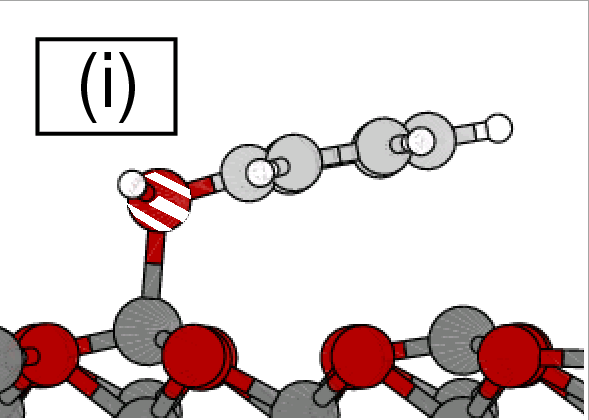	Adsorption of phenol on graphite(0001) and α-Al2O3(0001): Nature of van der Waals bonds from first-principles calculations (Chakarova-Käck, Borck, Schröder, Lundqvist) Physical Review B 74 (2006) 155402. Copyright (2006) by the American Physical Society.
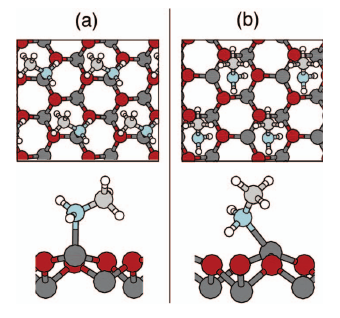	Adsorption of methylamine on alpha-Al2O3(0001) and alpha-Cr2O3(0001): Density functional theory, /Borck, Hyldgaard, and Schröder) Physical Review B 75, 035403 (2007). Copyright (2007) by the American Physical Society. The article was selected to simultaneously appear in the January 15, 2007 issue of the AIP/APS Virtual Journal of Nanoscale Science & Technology.
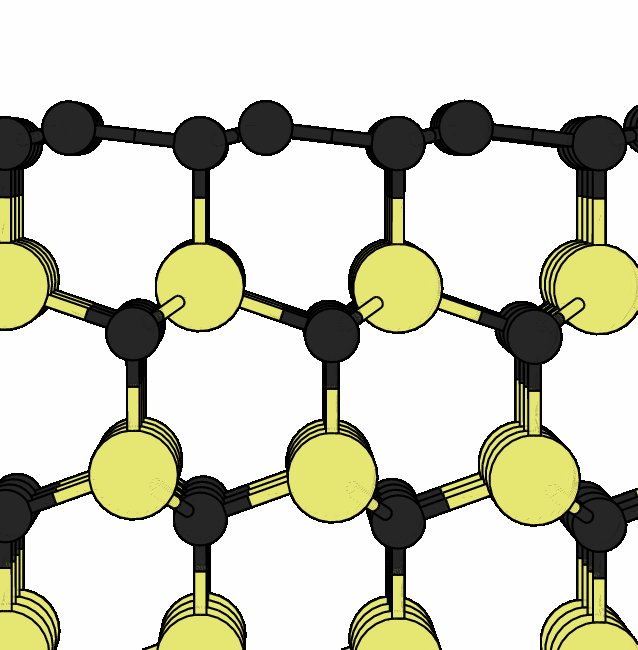	Relative stability of 6H-SiC(0001) surface terminations and formation of graphene overlayers by Si evaporation (Rohrer, Ziambaras, and Hyldgaard) Submitted to Physical Review B (in 2011). cond-mat/1102.2111.