Page: 1 2 3
4 5 6
7 8 9
10 11 12
13 14 15
16 17 18
1. Introduction
A Josephson junction is a structure consisting of two superconducting electrodes
separated by a thin insulating layer, usually of the order of 2 nanometers in
thickness. This structure is named after B.D. Josephson who predicted1 the
existence of a small current without any voltage drop. The junction is partly
characterized by its Josephson coupling energy 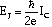 ,
where IC is the critical current, which is the maximum zero-voltage current
of the junction. If the junction is sufficiently small the charging energy
,
where IC is the critical current, which is the maximum zero-voltage current
of the junction. If the junction is sufficiently small the charging energy
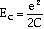 , where C is the capacitance
of the junction, becomes important. This is the energy stored in the electric
field of a capacitor C with the charge ±e on its electrodes. Thus if a Cooper
pair tunnels in an uncharged Josephson junction it will momentarily charge the
junction with the charge ±2e, increasing the energy by 4EC. In a single junction
this is usually not a problem because with some help from Heisenberg's
uncertainty law,
, where C is the capacitance
of the junction, becomes important. This is the energy stored in the electric
field of a capacitor C with the charge ±e on its electrodes. Thus if a Cooper
pair tunnels in an uncharged Josephson junction it will momentarily charge the
junction with the charge ±2e, increasing the energy by 4EC. In a single junction
this is usually not a problem because with some help from Heisenberg's
uncertainty law,  E
E t>
t> /2,
the charge slips quickly away from the junction, discharging
it before the energy conservation law notices. But if there is any obstacle
close after the junction, for example another junction or a resistor, the
junction might stay charged long enough for the energy law to catch up. Then the
tunneling will be suppressed and there will be no current without a little
voltage to help. This is called the Coulomb blockade2 of Cooper pair tunneling.
In a simple model,
/2,
the charge slips quickly away from the junction, discharging
it before the energy conservation law notices. But if there is any obstacle
close after the junction, for example another junction or a resistor, the
junction might stay charged long enough for the energy law to catch up. Then the
tunneling will be suppressed and there will be no current without a little
voltage to help. This is called the Coulomb blockade2 of Cooper pair tunneling.
In a simple model,  t is the discharge time for the capacitor,
t is the discharge time for the capacitor,
 t=ReC, where Re is the impedance of the junction
environment, assumed frequency independent. The condition for Coulomb blockade is then
4EC>
t=ReC, where Re is the impedance of the junction
environment, assumed frequency independent. The condition for Coulomb blockade is then
4EC> E>
E> /2
/2 t,
which implies
Re>
t,
which implies
Re> /4e2
/4e2 1 k
1 k .
.
In an array of Josephson junctions the tunneling behavior is partly determined
by the ratio of EJ to EC. If EJ >>EC
there will be no Coulomb blockade and the array will be superconducting. If, on the other hand,
EC>>EJ, there will be a clear Coulomb blockade.
If a magnetic field is applied perpendicular to the array the behavior can
usually be described in terms of frustration3,4, provided that the array is
homogeneous, i.e. the junctions, holes and superconducting "islands" are the
same in the entire array, and provided that the array is considerably smaller
than the Josephson penetration depth5 (several mm in this case). Frustration is
dimensionless and proportional to magnetic field. Frustration f=1 corresponds to
one flux quantum,  0=h/2e, in every loop in the array.
Properties that depend on frustration are periodic (f -> f+1) for sufficiently low
frustrations. At high enough fields other effects come into account, like the suppression
of superconductivity.
0=h/2e, in every loop in the array.
Properties that depend on frustration are periodic (f -> f+1) for sufficiently low
frustrations. At high enough fields other effects come into account, like the suppression
of superconductivity.
One interesting effect is the frustration dependence of the zero-bias resistance
(the resistance close to zero current), which decreases at integer as well as
rational frustrations (1/2, 1/3, 2/3 etc.). The resistance can change by five
orders of magnitude, just by changing the magnetic field slightly6,7.
The threshold voltage also changes with frustration, as one measurement in this
report shows. The threshold voltage is the minimum voltage required to start a
current in an array with Coulomb blockade.
4
<===Previous page ooo
Next page ===>
My homepage.
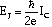 ,
where IC is the critical current, which is the maximum zero-voltage current
of the junction. If the junction is sufficiently small the charging energy
,
where IC is the critical current, which is the maximum zero-voltage current
of the junction. If the junction is sufficiently small the charging energy
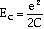 , where C is the capacitance
of the junction, becomes important. This is the energy stored in the electric
field of a capacitor C with the charge ±e on its electrodes. Thus if a Cooper
pair tunnels in an uncharged Josephson junction it will momentarily charge the
junction with the charge ±2e, increasing the energy by 4EC. In a single junction
this is usually not a problem because with some help from Heisenberg's
uncertainty law,
, where C is the capacitance
of the junction, becomes important. This is the energy stored in the electric
field of a capacitor C with the charge ±e on its electrodes. Thus if a Cooper
pair tunnels in an uncharged Josephson junction it will momentarily charge the
junction with the charge ±2e, increasing the energy by 4EC. In a single junction
this is usually not a problem because with some help from Heisenberg's
uncertainty law,  E
E t>
t> /2,
the charge slips quickly away from the junction, discharging
it before the energy conservation law notices. But if there is any obstacle
close after the junction, for example another junction or a resistor, the
junction might stay charged long enough for the energy law to catch up. Then the
tunneling will be suppressed and there will be no current without a little
voltage to help. This is called the Coulomb blockade2 of Cooper pair tunneling.
In a simple model,
/2,
the charge slips quickly away from the junction, discharging
it before the energy conservation law notices. But if there is any obstacle
close after the junction, for example another junction or a resistor, the
junction might stay charged long enough for the energy law to catch up. Then the
tunneling will be suppressed and there will be no current without a little
voltage to help. This is called the Coulomb blockade2 of Cooper pair tunneling.
In a simple model,  t is the discharge time for the capacitor,
t is the discharge time for the capacitor,
 t=ReC, where Re is the impedance of the junction
environment, assumed frequency independent. The condition for Coulomb blockade is then
4EC>
t=ReC, where Re is the impedance of the junction
environment, assumed frequency independent. The condition for Coulomb blockade is then
4EC> E>
E> /2
/2 t,
which implies
Re>
t,
which implies
Re> /4e2
/4e2 1 k
1 k .
. 0=h/2e, in every loop in the array.
Properties that depend on frustration are periodic (f -> f+1) for sufficiently low
frustrations. At high enough fields other effects come into account, like the suppression
of superconductivity.
0=h/2e, in every loop in the array.
Properties that depend on frustration are periodic (f -> f+1) for sufficiently low
frustrations. At high enough fields other effects come into account, like the suppression
of superconductivity.