The selling point of a multiprocessor is that you can apply the power of multiple CPUs to your program, so that it completes in less time. The preceding text in this document has been about making a program run faster in a single CPU. Now we start running the optimized program concurrently on multiple CPUs, and discover:
You can write a program that expresses parallel execution in the source code, or you can let the Power Fortran or Power C compiler find the parallelism that is implicit in a conventional, serial program.
When your program runs on more than one CPU, its total run time should be less. But how much less? And what are the limits on the speedup?
You can make your program run faster by distributing the work it does over multiple CPUs. There is always some part of the program's logic that has to be executed serially, by a single CPU. However, suppose there is one loop where the program spends 50% of the execution time. If you can divide the iterations of this loop so that half of them are done in one CPU while the other half are done at the same time in a different CPU, the whole loop can be finished in half the time. The result: a 25% reduction in program execution time.
The following topics cover the formal mathematical treatment of these ideas (Amdahl's law). There are two basic limits to the speedup you can achieve by parallel execution:
Tuning for parallel execution comes down to battling these two limits. You strive to increase the parallel fraction, p, because in some cases even a small change in p (from 0.8 to 0.85, for example) makes a dramatic change in the effectiveness of added CPUs.
And you work to ensure that each added CPU does a full CPU's work, and does not interfere with the work of other CPUs. In the Origin architectures this means:
There are two ways to obtain the use of multiple CPUs. You can write your source code to use explicit parallelism -- showing in the source code which parts of the program are to execute asynchronously, and how the parts are to coordinate with each other. Section 4.3 is a survey of the programming models you can use for this, with pointers to the online manuals.
Alternatively you can take a conventional program in C, C++ or Fortran, and apply a precompiler to it to find the parallelism that is implicit in the code. These precompilers, IRIS Power C and Power Fortran, insert the source directives for parallel execution for you. Section 4.4 is a survey of these tools.
If half of the iterations of a DO-loop are performed on one CPU, and the other half run at the same time on a second CPU, the whole DO-loop should complete in half the time. For example,
for (j=0; j<MAX; ++j) { z[j] = a[j]*b[j]; }
The IRIS Power C package can automatically distribute such a loop over n CPUs (with n decided at runtime based on the available hardware), so that each CPU performs MAX/n iterations.
The speedup gained from applying n CPUs, SpeedUp(n), is the ratio of the one-CPU execution time to parallel execution time: SpeedUp(n)=T(1)/T(n). If you measure the one-CPU execution time of a program at 100 seconds, and the program runs in 60 seconds with 2 CPUs, SpeedUp(2) = 100/60 = 1.67.
This number captures the improvement from adding hardware to the system. We expect T(n) to be less than T(1) -- if it is not, adding CPUs has made the program slower, and something is wrong! So we expect SpeedUp(n) to be a number greater than 1.0, and the greater it is, the more pleased we are. Intuitively you might hope that the speedup would be equal to the number of CPUs -- twice as many CPUs, half the time -- but this can never be achieved.
Normally, the number SpeedUp(n) must be less than n, reflecting the fact that not all parts of a program benefit from parallel execution. (When you go from 1 to 2 CPUs, the program does not run in half the time, so SpeedUp(n) is less than 2.0.) However, it is possible for just this to happen -- for SpeedUp(n) to be larger than m. This is called a superlinear speedup -- the program has been sped up by more than the increase of CPUs.
A superlinear speedup does not really result from parallel execution. It comes about because each CPU is now working on a smaller set of memory. The problem data handled by any one CPU fits better in cache, so each CPU executes faster than the single CPU could do. A hyperlinear speedup is welcome, but it indicates that the sequential program was being held back by cache effects.
It is a fundamental idea that there are always parts of a program that you cannot make parallel -- code that must run serially. For example, consider the DO-loop. Some amount of code is devoted to setting up the loop, allocating the work between CPUs. Then comes the parallel part, with all CPUs running concurrently. At the end of the loop there is more housekeeping that must be done serially; for example, if n does not divide MAX evenly, one CPU must execute the few iterations that were left over. The serial parts of the program cannot be speeded up by concurrency.
The mathematical statement of this idea is called Amdahl's law. Let p be the fraction of the program's code that can be made parallel (p is always a fraction less than 1.0.) The remaining (1-p) of the code must run serially. In practical cases, p ranges from 0.2 to 0.99.
The potential speedup for a program is proportional to p divided by the CPUs you can apply, plus the remaining serial part, (1-p):
1
SpeedUp(n) = ----------- (Amdahl's law: SpeedUp(n) given p)
(p/n)+(1-p)
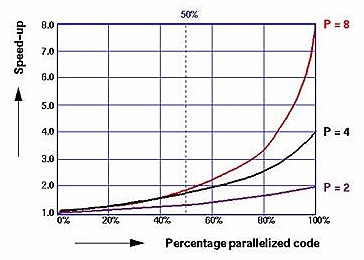
Suppose p=0.8; then SpeedUp(2)=1/(0.4+0.2)=1.67, and SpeedUp(4)=1/(0.2+0.2)=2.5. The maximum possible speedup -- if you could apply an infinite number of CPUs -- would be 1/(1-p). The fraction p has a strong effect on the possible speedup, as shown in this graph:

In particular, the more CPUs you have, the more benefit you get from increasing p. Using only 2 CPUs, you need only p=0.7 to get half the ideal speedup. With 8 CPUs, you need p=0.85 to get half the ideal speedup.
You do not have to guess at the value of F for a given program. Measure the execution times T(1) and T(2) to calculate a measured SpeedUp(2)=T(1)/T(2). The Amdahl's law equation can be rearranged to yield p when SpeedUp(n) is known:
2 SpeedUp(2) - 1
p = --- * -------------- (Amdahl's law: p given SpeedUp(2))
1 SpeedUp(2)
Suppose you measure T(1) = 188 seconds and T(2) = 104 seconds.
SpeedUp(2) = 188/104 = 1.81 p = 2 * ((1.81-1)/1.81) = 2*(0.81/1.81) = 0.895
In some cases, the SpeedUp(2)=T(1)/T(2) is a value greater than 2, in other words, a superlinear speedup (described earlier). When this occurs, the formula in the preceding section will return a value of p greater than 1.0, clearly not useful. In this case you need to calculate p from two other, more realistic, timings, for example T(2) and T(3). The general formula for p is:
SpeedUp(n) - SpeedUp(n)
p = -------------------------------------------
(1 - 1/n)*SpeedUp(n) - (1 - 1/m)*SpeedUp(m)
You can use this calculated value of p to extrapolate the potential speedup with higher values of N. For example, what is the expected time with 4 CPUs?
SpeedUp(4)= 1/((0.895/4)+(1-0.895)) = 3.04 T(4)= T(1)/SpeedUp(4) = 188/3.04 = 61.8
The calculation can be made routine using the computer. For example, following awk script, which you can copy and save as amdahl.awk, reads an input line containing at least two numbers that represent T(1), T(2), ... :
{
for (j=1;j<=NF;++j)
{ # save times T(n)
t[j] = $j
}
if (2==NF)
{ # use simple formula for p given T1, T2
s2 = t[1]/t[2]
p = 2*(s2-1)/s2
}
else
{ # use general formula on the last 2 inputs
sm = t[1]/t[NF-1]
sn = t[1]/t[NF]
invm = 1/(NF-1)
invn = 1/(NF)
p = (sm - sn)/( sm*(1-invm) - sn*(1-invn) )
}
if (p<1)
{
printf("\n#CPUs SpeedUp(n) T(n) p=%6.3g\n",p)
npat = "%5d %6.3g %8.3g\n"
# print the actual times as given and their speedups
printf(npat,1,1.0,t[1])
for (j=2;j<=NF;++j)
{
printf(npat,j,t[1]/t[j],t[j])
}
# extrapolate using amdahl's law based on calculated p
# first, for CPUs one at a time to 7
for (j=NF+1;j<8;++j)
{
sj = 1/((p/j)+(1-p))
printf(npat,j,sj,t[1]/sj)
}
# then 8, 16, 32, 64 and 128
for (j=8;j<=128;j=j+j)
{
sj = 1/((p/j)+(1-p))
printf(npat,j,sj,t[1]/sj)
}
}
else
{
printf("\np=%6.3g, hyperlinear speedup\n",p)
printf("Enter a list of times for more more than %d CPUs\n",NF)
}
}
The output for one line of input looks like:
% nawk -f amdahl.awk
106.0015 47.6993
p= 1.1, hyperlinear speedup
Enter a list of times for more more than 2 CPUs
106.0015 47.6993 33.5048 25.8661
#CPUs SpeedUp(n) T(n) p= 0.969
1 1 106
2 2.22 47.7
3 3.16 33.5
4 4.1 25.9
5 4.45 23.8
6 5.19 20.4
7 5.9 18
8 6.57 16.1
16 10.9 9.72
32 16.3 6.51
64 21.6 4.91
128 25.8 4.11
^D
These calculations are independent of most programming issues. They are not independent of hardware issues, because Amdahl's law assumes that all CPUs are equal. At some point of increasing N, adding a CPU no longer affects runtime in a linear way. For example, in the SGI Challenge architecture, most applications scale closely with Amdahl's law for n=2 through n=12, sometimes a few more. After that, the actual speedup is less than predicted. The added CPUs cannot run at full speed because the system bus is approaching saturation.
In the Origin2000 the situation is different, and better. Some benchmarks in the Origin scale very closely to Amdahl's law through n=32 and n=64 (larger configurations have not been tested at this writing). However it is important to remember that there are two cpu's per node, so some applications (in particular, applications with large local memory bandwidth requirements) follow Amdahl's law on a per node basis rather than a per cpu basis. Furthermore, not all added CPUs are equal because some are farther removed from shared data and thus may have a greater latency to access that data. In general, if you can locate the data used by a CPU in the same node or a neighboring node, the difference in latencies is slight, and the program speeds up in line with the prediction of Amdahl's law.
You can use a variety of programming models to express parallel execution in your source program. For a longer discussion of these models, see the online book Topics in IRIX Programming.
Your Fortran program can contain directives (specially-formatted comments) that request parallel execution. There are three families of directives:
Using PCF directives you can convert any block of code into a parallel region
to be executed by multiple CPUs concurrently. You can have different parts
of the region execute in different threads, or all threads can execute the
entire region. You can specify parallel execution of the body of a DO-loop.
There are directives that coordinate parallel threads, for example, to define
critical sections.
Using C$DOACROSS you can distribute the iterations of a single DO-loop across
multiple CPUs. You can control how the work is divided. For example, the
CPUs can do alternate iterations, or each CPU can do a block of iterations.
These directives complement C$DOACROSS, making it easy for you to distribute the contents of an array in different nodes so that each CPU is close to the data it uses in its iterations of a loop body.
All of these directives are discussed in the MIPSpro Fortran 77 Programmer's Guide and the MIPSpro Fortran 90 Programmer's Guide along with detailed instructions on their use. There are many variations possible in the use of these directives.
Your Fortran 77 or Fortran 90 program can exert direct control at runtime over the parallel library by calling the subroutines documented in the reference page mp(3F).
Your C or C++ program can contain directives (specially-formatted preprocessor lines that are also called pragmas) that request parallel execution. These pragmas are documented in detail in the C Language Reference Manual.
The C pragmas are similar in design to the PCF directives for Fortran. You use the pragmas to mark off a block of code as a parallel region. You can specify parallel execution of the body of a for-loop. Within a parallel region you can mark off statements that must be executed by only one CPU; this provides the equivalent of a critical section.
Your C/C++ program can exert direct control at runtime over the parallel library by calling the functions documented in the reference page mp(3C). Environment variables described in the reference page mp(3F) also apply to C programs.
There are two standard libraries, each designed to solve the problem of distributing a computation across not simply many CPUs, but across many systems, possibly of different kinds. Both are supported on Origin servers.
The MPI (Message-Passing Interface) library is designed and standardized at Argonne National Laboratory, and is documented on the MPI home page.
The PVM (Portable Virtual Machine) library is designed and standardized at Oak Ridge National Laboratory, and is documented on the PVM home page.
The SGI implementation of the MPI library generally offers better performance than the SGI implementation of PVM, and MPI is the recommended library. The use of MPI and PVM programs on SGI systems is documented in the online book MPI and PVM User's Guide.
You can write a multithreaded program using the POSIX threads model and POSIX synchronization primitives (POSIX 1003.1b, threads, and 1003.1c, realtime facilities). The use of these libraries is documented in the online book Topics in IRIX Programming.
Through IRIX 6.4, the implementation of POSIX threads creates a certain number of IRIX processes, and uses them to execute the pthreads. Typically the library creates fewer processes than the program creates pthreads (called an "m-on-n" implementation). You cannot control or predict which process will execute the code of any pthread at any time. When a pthread blocks, the process running it looks for another pthread to run.
You can write a multiprocess program using the IRIX sproc() function to create a share group of processes using a single address space. The use of the process model and shared memory arenas is covered in the book Topics in IRIX Programming.
Fortran and C programs that are written in a straightforward, portable way, without explicit source directives for parallel execution, can be parallelized automatically.
To do so, you invoke a source-level analyzer that inspects your program for loops that can be parallelized. The analyzer inserts the necessary compiler directives to request parallel execution. You can insert high-level compiler directives that assist the analyzer in marking up the source code. You typically repeat the compile several times before the analyzer recognizes all the parallelism that you believe is there.
These source analyzers are named, documented, and priced as if they were separate products: Power Fortran 77, Power Fortran 90, and IRIS Power C. However, when one of them has been installed in your system, it is integrated with the compiler. You can invoke the analyzer as a separate command, or you can invoke it as a phase of the compiler: for a Fortran 77 or Fortran 90 program, the -pfa ("Power Fortran Analyzer") compiler option; for a C program, the -pca ("Power C Analyzer") option to the cc command.
The analyzer processes the source program after the macro processor (cpp), and before the compiler front-end performs syntax analysis. The analyzer examines all loops and, when it can, it inserts compiler directives for parallel execution, just as if you had done so (see section 4.3.1 and section 4.3.2). The manuals that document this process are:
You should also examine the reference pages pfa(1) and pca(1).
This section assumes you have a working parallel program but are concerned about its performance. The section will outline, by increasing order of difficulty, the steps to go through to improve the parallel performance of your program. Some of the performance problems that arise on Origin2000 are the same as for the Challenge architecture, however many are specific to the NUMA nature of the Origin2000 memory system (see Shared Memory Without a Bus). Some familiarity with the memory architecture and parallel processing issues is assumed.
Before starting to tune your program, you must convince yourself that tuning is worthwhile. Presumably you have already done the single processor tuning. Now you run it in parallel and discover performance problems. Possibly perfex(1) reveals a high cost for memory access that is not present when running the program in a single CPU (see Profiling Tools). Most probably you find that the program does not scale as Amdahl's law predicts and must now undertake steps to resolve the performance problem. Below follows the questions to ask and steps to take to remedy a parallel performance problem.
If it is a message passing program, then you should determine what message passing library is being used. The current SGI implementations of MPI and PVM (from Array Services 2.0) are not NUMA aware. As a result the memory for all processes may end up being allocated on the same node, thus creating unnecessary contention for that node. On jobs with more than two processes you may observe (using top or gr_osview) the processes jumping around as each thread tries to execute on that one node holding its data. The solution is to use dplace described below to explicitly place the processes and memory of your program on the desired nodes. Most MPI implementations (including SGI's) use $MPI_NP+1 threads for a $MPI_NP processor job. The first thread is mostly inactive and should not be placed, so a typical placement file for an MPI application looks like:
# scalable placement_file for MPI # two threads per memory memories ($MPI_NP + 1)/2 in topology cube # set up memories threads $MPI_NP + 1 # number of threads distribute threads 1:$MPI_NP across memories # ignore the lazy thread
This example places two threads per memory where the memories are selected from a hypercube topology to reduce the number of router hops in remote references. $MPI_NP threads are distributed across the selected memories, and the first thread is left unplaced since it will be mostly inactive.
The design of the Origin2000 or Onyx2 memory system is discussed in an earlier section. The important point made there is that, in a system with 4 or more CPUs, the time to access some memory is greater than the time to access other memory. Therefore, if your program is to run as fast as possibly, the data it uses should be located in memory that is near to the CPU that executes the code.
At first this might seem to be a major performance issue, but for several reasons it is often not important at all:
Consequently if your program deals with no more than a few tens of megabytes
of memory and IRIX successfully allocated it in the local node, there may
be no performance problem.
Dynamic page migration is a conservative plan that has several restrictions.
However, if your program maintains stable memory-access patterns for periods
of minutes or more, IRIX adapts the memory configuration to make memory
local.
For these reasons, you may not need to spend any time on page placement issues at all.
When is page placement a problem? None of the counter values reported by perfex are diagnostic of memory access costs. This is a performance problem you have to diagnose by elimination. However, it is the most likely cause of poor parallel performance on Origin2000 and there exists a rich set of tools for correcting it.
If you have access to a Challenge system, then an almost certain indicator of a page placement problem is a program that exhibits good scalability on Challenge and poor scalability on Origin2000. In the more likely event that you don't have a Challenge system to test on, you can still suspect page placement is a problem if the program has one or more of the following characteristics:
In order to correct the problem you need to ensure two things:
If neither of these can be achieved, at least make sure that the data is distributed across multiple nodes to maximize memory bandwidth.
The first problem is an algorithmic issue. Ideally the data structures used by the program can be broken up at page boundaries into separate pieces that can be worked on independently by each parallel thread. It is not possible for a page of memory to be in two nodes at once consequently when a page is used simultaneously by two or more threads, that page will be closer to some threads than to others. Neither dynamic page migration, nor specific page placement can do anything with such a page. You can use the dprof(1) tool ( described earlier) to identify the pages being referenced by multiple threads and count the number of references made. If it is a large number, then you have an algorithmic problem that will require source code changes. If perfex shows a relatively small number of invalidations, then it is possible that the threads may actually be accessing different parts of the same page, and the problem is one of false page sharing (not to be confused with the more familiar cache line false sharing ) and can sometimes be remedied with the c$distribute_reshape directive described below .)
The second problem is a page placement issue. Even though the parallel threads all work on their own piece of data, these data may have been poorly placed on the system and so be causing a performance problem. A common example arises in porting SMP code to an S2MP architecture like Origin2000. Often in SMP code data are initialized in a serial part of the program and used in parallel sections further down. By default, data that are initialized serially are allocated on a single node, and this creates contention for that node's memory. The remedy is to place the pages near the threads that use them. The options available for diagnosing the usage patterns and placing the pages are as follows:
These items are described more fully below.
If you suspect poor page placement is affecting your parallel performance and you cannot modify the code, then try using dplace(1) to distribute your processes and data. The dplace(1) command executes a specified program, initializing the processes and memory of that program on the nodes that you specify. The details of dplace are covered in its reference pages, all three of which you should print and save for reference:
dplace is most commonly used on the command line to control the placement of threads and data without making source code changes. It can also be called from within a program (see the dplace(3) reference page), a feature that is useful for dynamic control of page migration.
To place data according to the file placement_file for the executable a.out that would normally be run by:
% a.out < in > out
you would simply enter:
% dplace -place placement_file a.out < in > out
An example placement file was given above for MPI programs. The dplace reference pages give more examples of placement files, and dplace(5) in particular is devoted to describing the construction of placement files.
As a command line tool used in the manner described above, dplace can do the following:
If you want to use dplace to place specific ranges of memory, then the dprof(1) tool described earlier can be very useful.
The -mustrun switch is useful for obtaining benchmark performance but should be avoided in a multi-user environment.
You can use dplace to execute any programs, except that MPI and PVM programs must be started by their respective run commands.
You cannot use dplace to associate memory segments with particular POSIX threads because of the unpredictable relationship between pthreads and processes. However, you can use dplace to launch a pthread program for other reasons, for example to specify page size.
Before starting programs linked with libmp, you should set the environment variable _DSM_OFF so that libmp and dplace will not do conflicting things.
When a program begins, the IRIX kernel will create a Memory Locality Domain or MLD for each process and try to place it on the same node as is executing the process. When a process initializes memory, the kernel locates the new memory pages in the node storing the MLD for the process. In the majority of cases this is the same node where the process is executing. This default rule (often referred to as first touch) has the following implications:
Each child process should allocate any memory areas that it uses exclusively.
Those areas will be located in the node where that process runs.
The default allocation policy can cause a performance problem in two cases:
You can address the second problem without source code changes by forcing an alternative method of allocation: round robin in all nodes. To do this, set a nonempty value in the environment variable _DSM_ROUND_ROBIN prior to executing a program that is linked with libmp. Each successive memory allocation is located in a different node. This does not locate the data in the optimal location -- each process has 1/number-of-nodes chance of being in the same node as the data it uses. However, memory access is spread across many nodes, and the node of the parent process is not a bottleneck. If it is a long enough running job, then you can also turn on automatic page migration to eventually move pages to the appropriate nodes. Note that the optimal solution is to modify the source code and either parallelize the initialization loops or place the data explicitly with the appropriate compiler directives. However when source code changes are impossible, then using round robin allocation, possibly in combination with automatic page migration, is a good alternative.
The initial distribution of data that you create by default, or by using dplace or compiler directives, may not be correct for all phases of the program. In general, when a program switches from one stable pattern of memory access to another stable pattern, you want data pages to migrate to the nodes where they are needed. A common example of this is found in SMP code where the data for a program may have all been initialized in a serial portion, and the parallel sections occur further down. Data that is initialized serially will be allocated on a single node, so this creates contention for that node's memory. By using automatic page migration (for this case, in combination round robin page allocation) you can remedy this common performance problem.
The IRIX automatic page migration facility is disabled by default because page migration is an expensive operation that impacts all CPUs, not just the ones used by the program whose data is being moved. Some programs shift their access patterns rapidly, which would cause excessive page migration. You can enable dynamic page migration for a specific program in the following ways:
When you can make source changes in the program, you can call dplace functions directly from the program in order to:
You can use these abilities in two ways:
The SGI Fortran 77 compiler (version 7.x) honors compiler directives for data placement. These directives are covered in detail in Chapter 6: Parallel Programming on Origin2000 of the MIPSpro Fortran 77 Programmer's Guide for IRIX 6.4. In summary, the directives are as follows:
| Directive | Purpose |
| c$distribute A(<dist>,<dist>,) | Declares static distribution of array by pages. |
| c$dynamic A | Declares an array can be dynamically redistributed at runtime. |
| c$distribute_reshape B(<dist>,<dist>,) | Declares static reshaping of array regardless of page boundaries. |
| c$redistributeA(<dist>,<dist>,) | Executable statement that redistributes array at runtime. |
| c$page_place A(<addr>,<sz>,<thread>) | Declares specific placement of range of addresses to thread. |
| c$doacross affinity(i) = data(A(i)) | Clause that puts loop iterations on the node that owns the data used in that iteration. |
| c$doacross affinity(i) = thread(<expr>) | Clause that assigns loop iterations to threads based on the induction variable. |
| c$doacross nest(i,j) | Clause that allows perfectly nested parallel loops. |
| c$distribute OR c$doacross nest onto | Clause to specify processor topology to either c$distribute or c$doacross nest. |
The Fortran 77 programmer can use these directives to locate blocks or stripes of arrays in the same Origin nodes that execute the threads that use those parts of the arrays. The c$distribute and c$redistribute directives operate at a high level; you only need to know how the relevant DO-loop is parallelized. You should not use the data affinity clauses to c$doacross unless you have also taken care to distribute the data.
The c$distribute, c$redistribute, and c$page_place directives all work on pages of data. When you specify a distribution with these directives, the compiler applies the distribution as best as it can without breaking pages. For this reason there is little runtime overhead with these directives. On the other hand, these directives are useful only when each thread's piece of data is substantially larger than a page size (minimum of 16 KBytes on Origin2000).
The c$distribute_reshape directive tells the compiler it may break pages to obtain the specified distribution. In other words, the compiler will change the layout of the specified arrays at the cost of sequentiality of memory. As a result there can be greater runtime overhead (in the form of integer divides and modulo's) for address calculations. Also note that once a shape is specified, it remains for the duration of the program. Therefore you should use this directive only if the distribution is static. There are some additional restrictions to the use of c$distribute_reshape as outlined in the section on Types of Data Distribution in Chapter 6: Parallel Programming on Origin2000 of the MIPSpro Fortran 77 Programmer's Guide for IRIX 6.4.
The c$distribute_reshape directive is useful for resolving problems of false page sharing. Data that would normally lie on the same page referenced by two different threads can be put on two different pages with this directive. Consider for example distributing the columns of a matrix for parallel Gaussian elimination. The code may look like:
c$distribute A (*, CYCLIC(1))
C Perform Gaussian elimination across columns
C The affinity clause distributes the loop iterations based
C on the column distribution of A
do i = 1, n
c$doacross affinity(j) = data(A(i,j))
do j = i+1, n
... reduce column j by column i ...
enddo
enddo
Here we have used a cyclic distribution, by pages, of the columns of A. However if the columns are smaller than a page, then we'll have multiple columns placed on a node that need to be referenced by remote processors. By changing the keyword distribute to distribute_reshape we can break the pages such that each column is stored on the node where it will be referenced.
Another situation where reshaping is useful occurs when the desired distribution is contrary to the layout of the array. For example, suppose you have a rectangular domain on which you're solving a simple diffusion equation. To minimize the number of remote references (i.e. communication), you may want to break the domain parallel to the shorter side.
real*8 A(m,n)
C m>n, so distribute ROWS of A in block fashion
c$distribute_reshape A (BLOCK, *)
c$doacross local(j) affinity(i) = data(A(i,j))
do i = 1,m
do j = 1,n
... apply diffusion operator on A(i,j) ...
enddo
enddo
Note that this example is somewhat contrived. You may well find that the cost of local cache misses from striding (the j loop is innermost) outweighs the benefit from reducing remote references.
Using c$page_place, you can dynamically locate any segment of memory in a specific node. In order to use this powerful directive, you have to know in detail how many threads are executing, and which thread is using what data.
As of the 7.1 compiler release, most of the equivalent #pragmas have not been implemented for the C language. However, the #pragma page_place, equivalent to c$page_place, has been implemented and is documented in the C Language Reference Manual.
Cache contention can arise in any multiprocessor including the SGI Challenge series but is discussed here in the context of Origin2000. Cache contention is an issue only for data that are frequently updated or written. Data that are mostly read and rarely written do not cause cache contention.
The scheme used by the Origin2000 to maintain cache coherence was described earlier. When one CPU modifies a cache line, any other CPU that has a copy of the same cache line is notified, discards its copy, and fetches a new copy when it needs that data again. This can cause performance problems in two cases:
In both cases, perfex will reveal a high number of cache invalidation events (hardware counters 13, 28, and 29 -- see the perfex description). The CPU or CPUs doing the updating show a high count of stores to shared cache lines (counter 31).
You deal with cache contention by changing the layout of data in the source program. You may have to make algorithmic changes as well. Examine each parallel region of the program: any assignment to memory in a parallel region is suspect. You must ask, is that variable, or is data adjacent to that variable in memory, used by other CPUs at this time? If so, the assignment forces the other CPUs to read a fresh copy of the cache line. Synchronization objects may also be a cause of cache contention.
In general terms, your strategies are:
An update of one word invalidates all the 31 other words in the same cache line. When the other words are not related to the new data, you have false sharing -- variables that are invalidated and will have to be reloaded from memory merely by the accident of their address, without logical need. One way to discourage false sharing is to create data structures that are multiples of a cache line in size, and to allocate them on cache-line boundaries in memory.
Be careful if your program has a block of global status variables that is visible to all parallel threads. In the normal course of the program, every CPU will have a cached copy of all or most of this common area. Shared, read-only access does no harm. But if items in the block are volatile (frequently updated), those cache lines are invalidated often. For example, a global status area might contain the anchor for a LIFO queue of some kind. Each time a thread puts or takes an item from the queue, it updates the queue head -- invalidating a cache line.
It is inevitable that a queue anchor field will be frequently invalidated. However, the time cost can be isolated to queue access by applying strategy 2. Allocate the queue anchor in separate memory from the global status area. Put a pointer to it (a non-volatile item) in the global status block. Now the cost of fetching the queue anchor is born only by CPUs that access the queue. If there are other items that are updated with the queue anchor -- such as a lock that controls exclusive access to the queue -- place them adjacent to the queue, aligned so that all are in the same cache line (strategy 4). However, if there are two queues that are updated at unrelated times, place each in its own cache line (strategy 3).
Synchronization objects such as locks, semaphores, and message queues are global variables, and must be updated by each CPU that uses them. You may as well assume that these objects are always accessed at memory speeds -- not cache speeds. You can do two things to reduce contention:
When you make a loop run in parallel using C$DOACROSS, try to ensure that each CPU operates on its own distinct sections of the input and output arrays. Compiler directives exist for this purpose.
Carefully review the design of data collections that are used by parallel code. For example, the root and the first few branches of a binary tree are likely to be visited by every CPU that searches that tree -- and will be cached by every CPU. However, elements at higher levels in the tree may be visited by only a few CPUs. You might pre-build the top levels of the tree so that these levels never have to be updated once the program starts. Also, before you implement a balanced-tree algorithm, consider that tree-balancing can propagate modifications all the way to the root. It might be better to cut off balancing at a certain level and never disturb the lower levels of the tree. (Similar arguments apply to B-trees and other branching structures: the "thick" parts of the tree are widely cached, while the twigs are less so.)
Other classic data structures can cause memory contention. Examples: